Деление окружности
Чтобы разделить окружность на четыре равные части, проводят два взаимно перпендикулярных диаметра: на пересечении их с окружностью получаем точки, разделяющие окружность на четыре равные части (рис. 31, а).
Чтобы разделить окружность на восемь равных частей, дуги, равные четвертой части окружности, делят пополам. Для этого из двух точек, ограничивающих четверть дуги, как из центров радиусов окружности выполняют засечки за ее пределами. Полученные точки соединяют с центром окружностей и на пересечении их с линией окружности получают точки, делящие четвертные участки пополам, т. е. получают восемь равных участков окружности (рис. 31, б).
На двенадцать равных частей окружность делят следующим образом. Делят окружность на четыре части взаимно перпендикулярными диаметрами. Приняв точки пересечения диаметров с окружностью А, В, С, D за центры, величиной радиуса проводят четыре дуги до пересечения с окружностью. Полученные точки 1, 2, 3, 4, 5, 6, 7, 8 и точки А, В, С, D разделяют окружность на двенадцать равных частей (рис. 31, в).
Пользуясь радиусом, нетрудно разделить окружность и на 3, 5, 6, 7 равных участков.
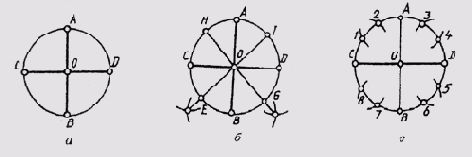
Рис. 31