Элементы трехпроекционного комплексного чертежа точки
Для определения положения геометрического тела в пространстве и получения дополнительных сведений на их изображениях может возникнуть необходимость в построении третьей проекции. Тогда третью плоскость проекций располагают справа от наблюдателя перпендикулярно одновременно горизонтальной плоскости проекций П1 и фронтальной плоскости проекций П2 (рис. 62, а). В результате пересечения фронтальной П2 и профильной П3 плоскостей проекций получаем новую ось П2/П3, которая располагается на комплексном чертеже параллельно вертикальной линии связи A1A2 (рис. 62, б). Третья проекция точки А — профильная — оказывается связанной с фронтальной проекцией А2 новой линией связи, которую называют горизонталь-
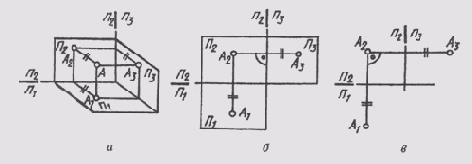
Рис. 62
ной. Фронтальная и профильная проекции точки всегда лежат на одной горизонтальной линии связи. Причем A1A2 _|_ А2А1 и А2А3, _|_ П2/П3.
Положение точки в пространстве в этом случае характеризуется ее широтой — расстоянием от нее до профильной плоскости проекций П3, которое обозначим буквой р.
Полученный комплексный чертеж точки называется трехпроек-ционным.
В трехпроекционном чертеже глубина точки АА2 проецируется без искажений на плоскости П1и П2 (рис. 62, а). Это обстоятельство позволяет построить третью — фронтальную проекцию точки А по ее горизонтальной А1 и фронтальной А2 проекциям (рис. 62, в). Для этого через фронтальную проекцию точки нужно провести горизонтальную линию связи A2A3 _|_A2A1. Затем в любом месте на чертеже провести ось проекций П2/П3 _|_ А2А3, измерить глубину f точки на горизонтальном поле проекции и отложить ее по горизонтальной линии связи от оси проекций П2/П3. Получим профильную проекцию А3 точки А.
Таким образом, на комплексном чертеже, состоящем из трех ортогональных проекций точки, две проекции находятся на одной линии связи; линии связи перпендикулярны соответствующим осям проекций; две проекции точки вполне определяют положение ее третьей проекции.
Необходимо отметить, что на комплексных чертежах, как правило, не ограничивают плоскости проекций и положение их задают осями (рис. 62, в). В тех случаях, когда условиями задачи этого не требу-
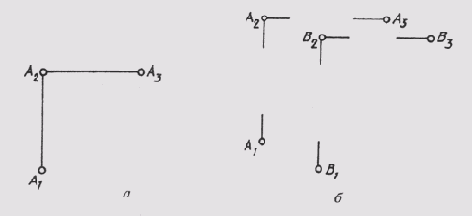
Рис. 63
ется, проекции точек могут быть даны без изображения осей (рис. 63, а, б). Такая система называется безосновой. Линии связи могут также проводиться с разрывом (рис. 63, б).
