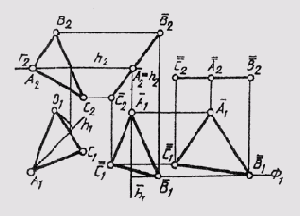
Треугольник ABC занимает общее положение. Первым плоскопараллельным перемещением он поставлен во фронтально проецирующее положение с помощью горизонтали h, которую расположим как фронтально проецирующую прямую в ее плоскости вращения Г || П. При этом А1В1С1 = А1В1С1, а плоскости вращения точек В и С параллельны плоскости Г.
Вторым перемещением АВС расположен параллельно плоскости П1. Без изменения оставлена вырожденная фронтальная проекция треугольника (А2В2C2 = А2В2С2), а новая горизонтальная проекция, дающая истинную величину АВС, получена построением новых горизонтальных проекций то-
Рис. 117
Рис. 118
чек А1В1 и С1 в результате их вращения в параллельных фронтальный плоскостях уровня (B2 ~ Ф; B ~ Ф).
На этом примере построено решение третьей и четвертой исходных задач путем преобразования комплексного чертежа плоскости общего положения способом плоскопараллельного перемещения.
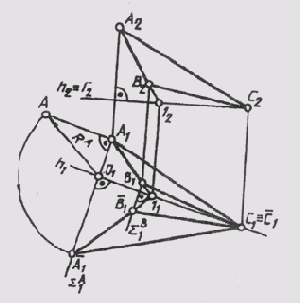
Если в качестве оси вращения взять линию уровня, то истинную величину плоской фигуры общего положения можно построить одним поворотом, т. е. избежать двойного преобразования чертежа, что имело место в замене плоскостей проекций и плоскопараллельном перемещении. На рис. 118 построено изображение АВС (А1В1С1) после поворота его вокруг горизонтали h (С, 1) уровня Г ~ h. Так как горизонталь проходит через точку С, то последняя неподвижна при вращении треугольника. Нужно повернуть только точки А и В вокруг горизонтали до совмещения с плоскостью Г || П1. Точка А вращается в горизонтально проецирующей плоскости SumА, перпендикулярной оси вращения. Центр вращения О точки А лежит, на оси вращения. В момент, когда в результате вращения точка А окажется в плоскости Г, т. е. совместится с горизонтальной плоскостью уровня, ее горизонтальная проекция А1 будет удалена от горизонтальной проекции оси вращения h1 на расстояние, равное истинной величине радиуса вращения RА точки А. Натуральную величину RА можно построить как гипотенузу О\А прямоугольного треугольника (см.